Ukázky úloh
Kategorie MŠ + A1 + A2
1.
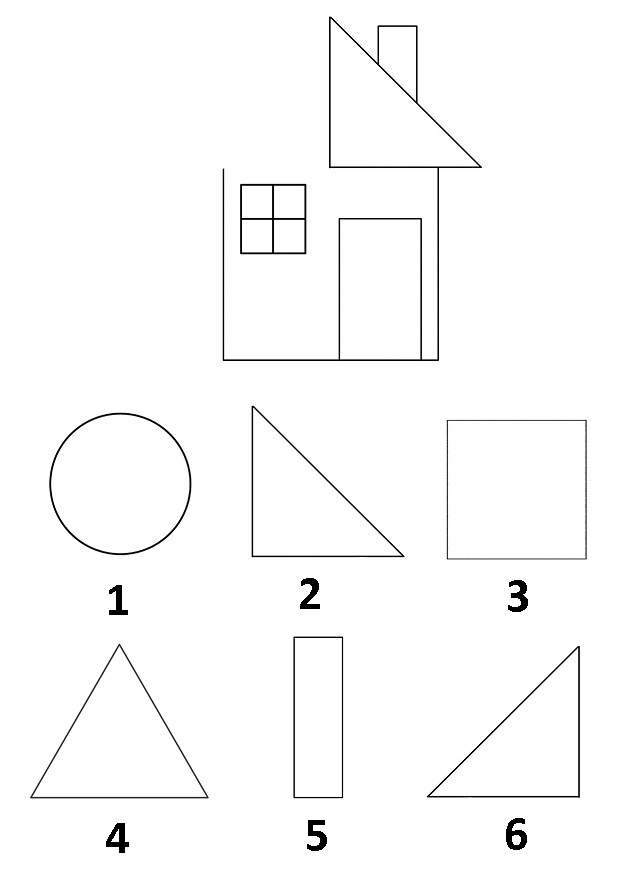
2.

3.

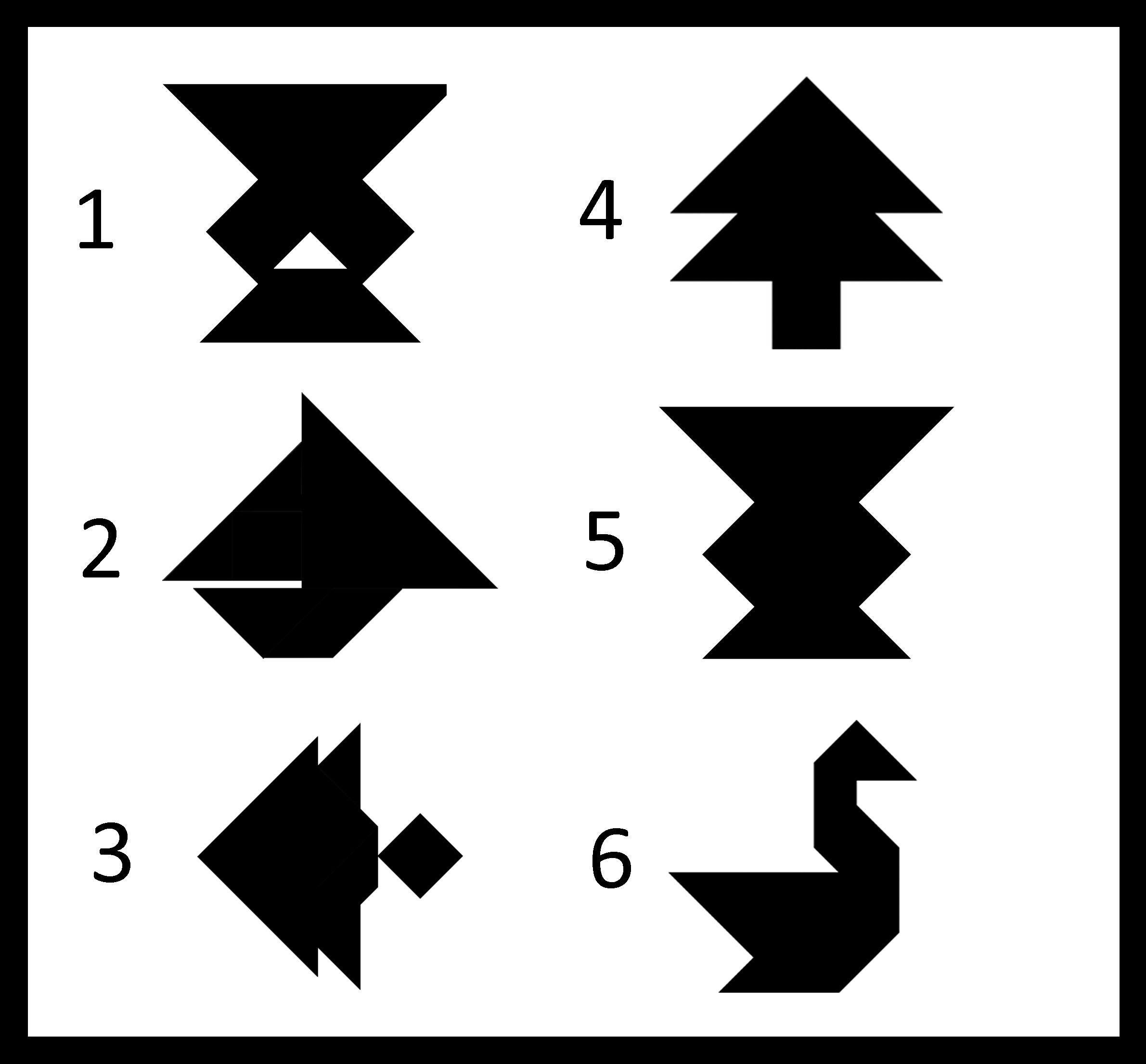
4.

5.
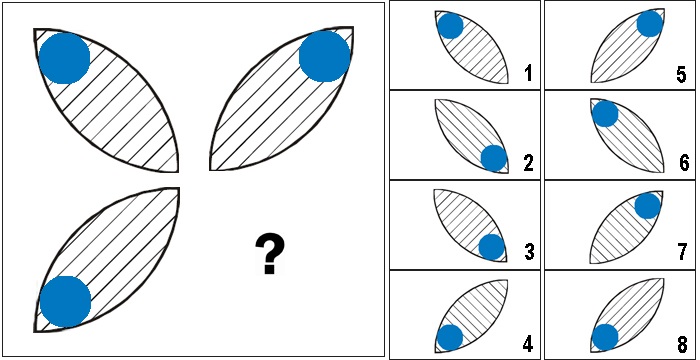
6.
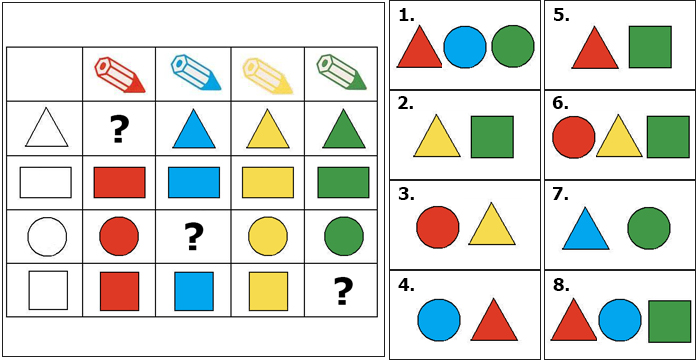
7.

Kategorie A
1. V pokladničce máš 264 Kč. Suma je tvořena pouze českými mincemi (1 Kč, 2 Kč, 5 Kč, 10 Kč, 20 Kč, 50 Kč), všech mincí máš stejný počet, kolik máš celkem mincí?
2.

3.

4. Lence je 14 let, její mamince 41. Čísla jsou zapsána stejnými číslicemi, ale v opačném pořadí. Nastane tento jev ještě někdy? Kdy nejdříve se tak stane?
5. "Nakreslete jedním tahem". Žluté čtverce slouží pro zapsání pořadového čísla průchodu uzlem.
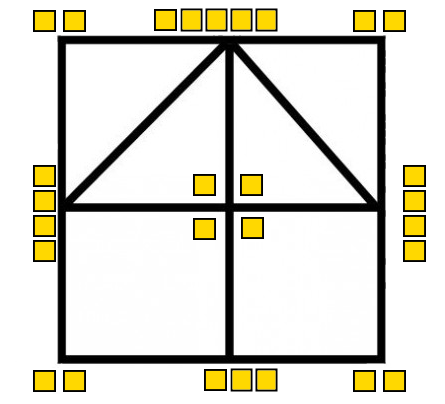
6.
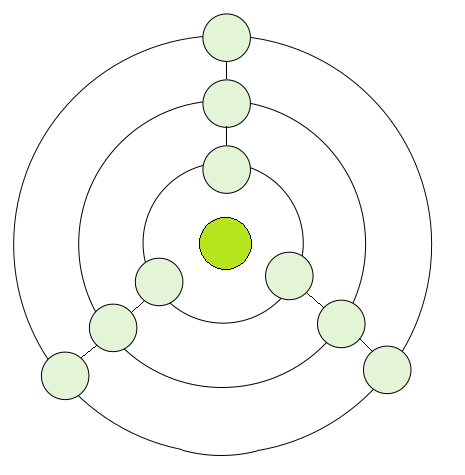
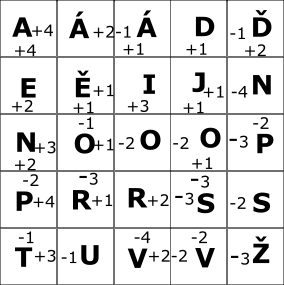
Do obrázku doplň číslice od nuly do 9 tak, aby v každém paprsku i na každé kružnici byl součet čísel 12. Střed se do součtu nezapočítává, tam doplň zbývající číslo. Žádná číslice se nesmí vyskytnout dvakrát.
7. Palindromem nazýváme číslo, které čteme zleva i zprava stejně. Například číslo 1 331 je palindrom. Na tachometru v autě je číslo 15 951. Kolik nejméně kilometrů musí auto ujet, aby číslo na tachometru bylo znovu palindrom?
Kategorie B
1. Kolik uběhlo minut od 12:00, jestliže právě před 2 hodinami uběhl přesně trojnásobný počet minut od 9:00?
2. Je mi pětkrát tolik, kolik bylo vám, když mně bylo tolik, jak jste nyní stár. Až vám bude tolik, kolik je dnes můj věk, budeme mít oba spolu 96 let. Kolik je nyní každému z mužů let?
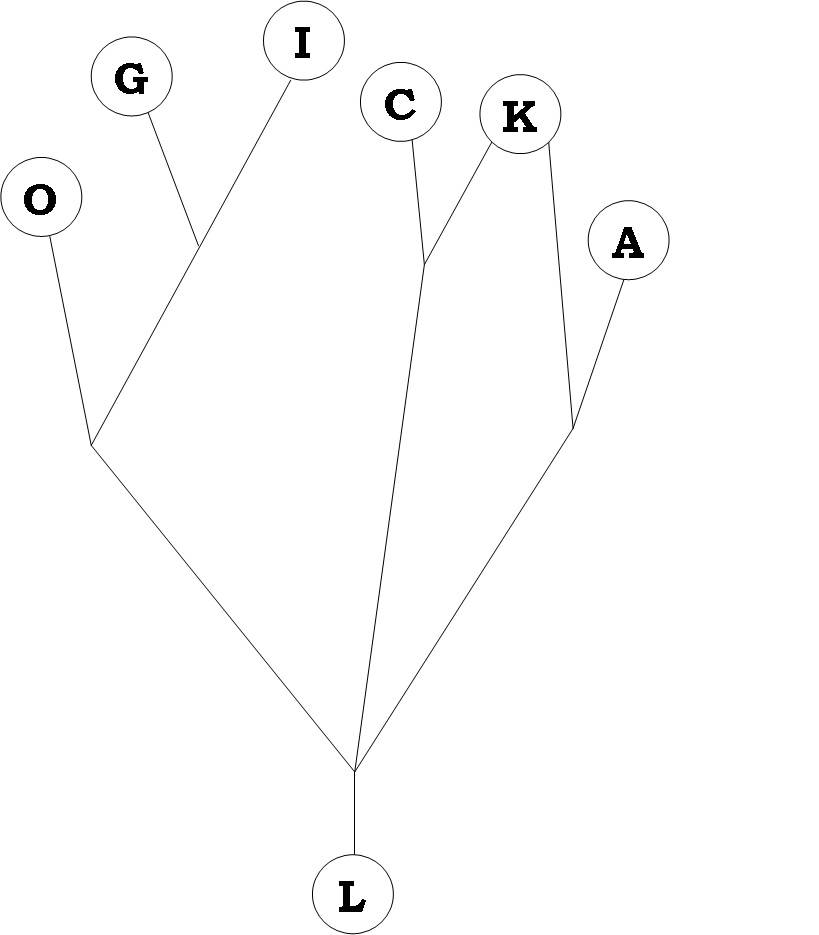
3. Poutníci ve hře "Bloudíme s Mensou" vyrazí vždy z města L, jdou po cestě a pokaždé, když dojdou na rozcestí, pokračují náhodně po některé z ostatních cest vedoucích z tohoto rozcestí (tedy se stejnou pravděpodobností). Vašim úkolem je určit, s jakou pravděpodobností skončí v jednotlivých městech, tedy pokud vyjde z města L milion poutníků, kolik dojde do kterého města?
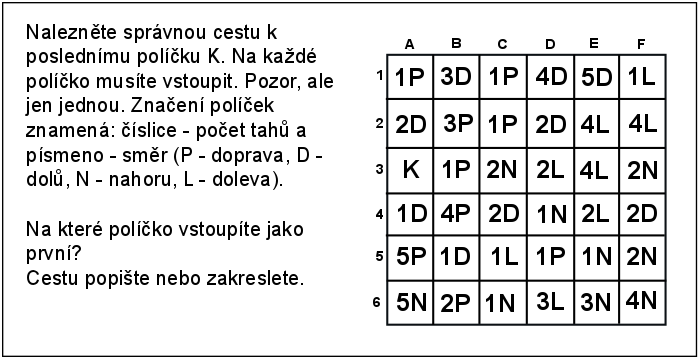
4.
5. Číslo 100 zapiš pomocí všech číslic od 1 do 9 a znamének pro sčítání a odčítání. Pořadí číslic od 1 do 9 je zachováno vzestupně nebo sestupně. Najdeš více jak jedno vzestupné a jedno sestupné řešení?
6. Do prázdných políček doplňte všechna čísla z řady od 1 do 18 tak, aby svisle platily početní úkony.
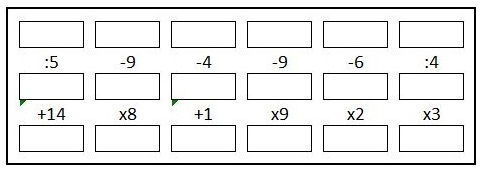
7.
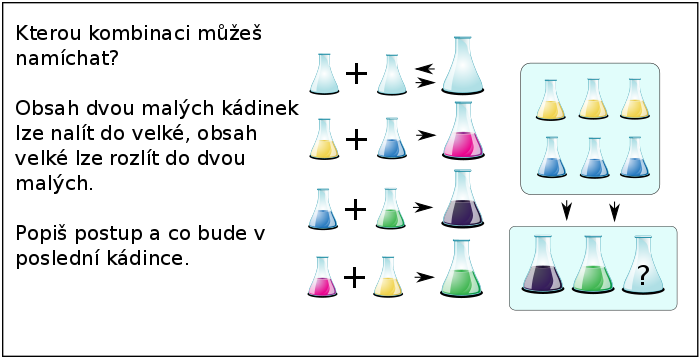
Jaká odpověď se skrývá v obrázku?
Jana bydlí v 5. patře a nejde do 5. třídy.
Do 3. třídy půjde Petr.
Dívka bydlící ve 3. patře není Zdeňka a chodí do 4. třídy.
Karel bydlí ve 4. patře.
Petr nebydlí ve 2. patře.
Urči, kdo chodí do které třídy a ve kterém patře bydlí.
Kategorie C
1. Doplň řadu 4 - 9 - 2 - 1 - 0 - 8 - 5 - ? - ? - ?
2. Mimozemšťané hledají planetu, kde by se usídlili. Prozkoumali 60 planet a zjistili, že šestina jich je moc daleko od slunce, třetina moc blízko, čtvrtina má málo vody, jedna pětina moc nízkou gravitaci a dvakrát tolik zase moc vysokou.
Kolik mohli maximálně najít zcela obyvatelných planet, pokud víme, že každá planeta splňuje alespoň jedno kritérium obyvatelnosti?
3. Najděte pokračování číselné řady: 11, 20, 38, 74, 146, ?
4. Poutníci ve hře "Bloudíme s Mensou" vyrazí vždy z města M, jdou po cestě a pokaždé, když dojdou na rozcestí, pokračují náhodně po některé z ostatních cest vedoucích z tohoto rozcestí (tedy se stejnou pravděpodobností). Silnější i slabší čáry označující cesty v obrázku jsou rovnocennými cestami. Vašim úkolem je určit, s jakou pravděpodobností poutníci skončí v jednotlivých městech. Pokud vyjde z města M milion poutníků, kolik dojde do kterého města?
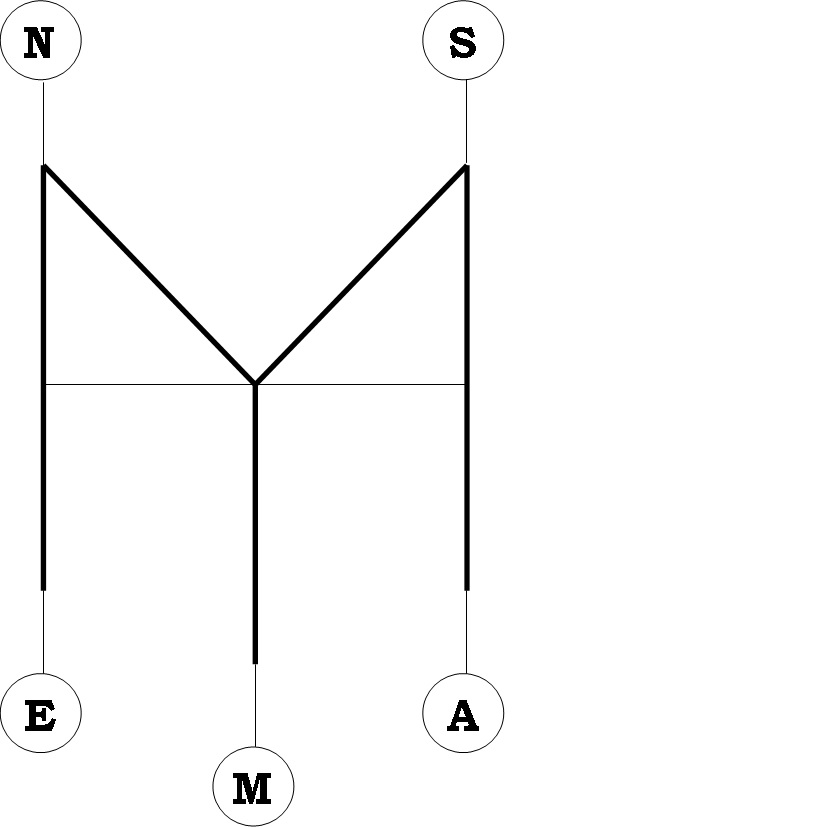
5.
6. O podvodníkovi a důvěřivci: Podvodník dal důvěřivci nabídku: „Udělej stojku a já ti peníze, které máš v kapse, zdvojnásobím. Za to mi dáš odměnu 16 Kč, opět uděláš stojku, peníze opět zdvojnásobím, dáš mi zase odměnu 16 Kč, a tak budeme pokračovat, jak dlouho budeš chtít.“ Důvěřivec byl však po čtvrtém kole bez peněz. Kolik korun měl na začátku? Jak by to dopadlo, kdyby měl původně v kapse o 1 korunu víc, než měl?
7. Do prázdných políček dopište chybějící čísla tak, aby každé číslo bylo jiné. Ve všech řadách nad základní řadou je každé číslo dáno součtem dvou čísel, která se nacházejí bezprostředně pod ním. Součet osmi čísel základní řady je 98.
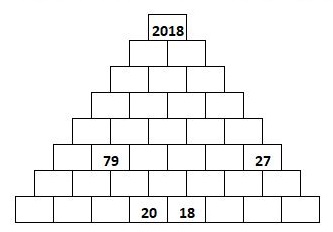
8.
V roce 1968, v den svých 40. narozenin, řekl pan Novotný:
"Znásobíme-li dnešní poslední den v měsíci počtem kol aut a motocyklů, které stojí v naší ulici, dostaneme číslo 812."
Kdy bude panu Novotnému 60 let?
Co bude napsáno v posledním řádku?


























